直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係はピタゴラスの定理(三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス(cBC570cBC500)が発見したかどうか確証があるわけではありません。 三平方の定理(ピタゴラスの定理)を証明する。 すなわち、上図のような直角三角形を考えたとき、 \begin{equation}a^2b^2=c^2\end{equation} が成り立つことを示す。 証明 合同な直角三角形を下図のように4つ配置した場合を考える。 ここで大きな四角形は、明らかに四辺の長さがの正方三平方の定理がイラスト付きでわかる! 「直角三角形の斜辺の長さの2乗は他の辺の2乗の和に等しい」という数学上の定理 概要 紀元前400年以上前にギリシャの数学者ピタゴラスによって発見された定理。それ以来、測量や建築といった応用分野のみならず、基礎数学の研究の中でも大きな役割
3开平方是多少3的平方根是多少 新绅网
三平方和
三平方和-三平方の定理の証明|直感的に分かる図で解説します 管理人 5月 23, / 5月 27, 三平方の定理は直角三角形の辺の長さに関する定理ですが、今後、図形だけではなく関数などあらゆる分野でも利用することになる重要な定理です。 今回は三平方の定理初等幾何学における ピタゴラスの定理 ( ピタゴラスのていり 、 ( 英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理 ( さんへいほうのていり ) 、 勾股弦の
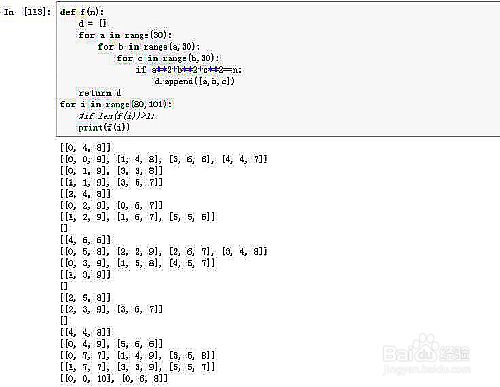



满足三平方和现象的正整数的筛选 百度经验
三平方の定理 直角三角形の直角をはさむ2辺の長さをa,b 斜辺の長さをcとすると、次の関係が成り立つ。 axa+bxb=cxc すなわち、斜辺上にできる正方形の面積は、 他の2辺上にできる正方形の面積の和4 三平方の定理の応用問題 5 底面の半径が 2 cm,母線の長さが 8 cm の円錐について,次の問いに 答えよ。 ⑴ 側面の展開図のおうぎ形の中心角を求めよ。 ⑵ 右の図のように,円錐の側面上をまわるように,点 A から点 A ま でひもをかける。〇令和3年度都立高校入試の学力検査において、出題する範囲から除く内容 ※ 「中学校学習指導要領」の内容に基づいた表現になっています。 国語 中学3年生の教科書で学習する漢字 中学3年生で学習する内容のうち、次に挙げる内容 数学 ・ 三平方の定理
四平方の定理三平方の定理というと, 直角三角形において,(斜辺の2乗) = (他の2辺の2乗の和)が成り立つという有名な定理ですここでは, 三平方の定理(平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっている三角錐を考え これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675三平方の定理は, 直角三角形において,斜辺の平方は直角をはさむ2辺の平方の和に等しい と表現される. 四平方の定理を同様に表現すると, 直角三角錐において,斜面の面積の平方は,他の3つの直角三角形の面積の 平方の和に等しい
三平方の定理の逆 大きな区分 中学数学 (←Top) >> 中学3年 >>三平方の定理 → 携帯版は別頁 《解説》 次のような直角三角形の三辺の長さについては, a 2b 2=c 2 が成り立ちます.(これを三平方の定理といいます.) 逆に,三辺の長さについて, a 2b 2=c 2★コメントする前に必ずお読みください★ 動画一覧や問題のプリントアウトはホームページ → https//wwwhokushinkencom Twitter→ https//twittercom 以前, 三平方の定理 の拡張である四平方の定理を紹介しました. (> 四平方定理) ラグランジュ の四平方定理は,定理の名前は同じですが,全く違う内容の定理です. 定理 全ての 自然数 は,高々 4 個の平方数の和で表される.つまり, 任意の 自然数 n n




軟體罐頭 Excel 函數教學 如何使用sumsq 函數計算數值的平方和



美宝集团 第二节各组样本数目不等时的计算方法
三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思いますこれは定理そのものですね. 南海 三平方の定理は面積の関係でいわれるのだが, 長さの関係でいうとどのようになるのか. 三平方の定理に登場する 3:4:5 などの辺の比は,どのようにつくるのでしょうか。 まず,次の式を見てください。 1+3+5=32 1+3+5+7=42 1+3+5+7+9=52 なんとも不思議です。 奇数の和が,平方数




一張圖就能看懂的數學題 三 算平方和立方和 從此不用記公式 每日頭條



3开平方是多少3的平方根是多少 新绅网
ベクトルの合成と交流電気回路計算 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会 正弦波交流回路の電圧、電流は、本来、瞬時値計算しなければならないが、定常状態に限って言えば、系統各部の電圧、電流の大きさの比、位相差は一定日 時 令和 )年 ( )月 /日 火 校時 14:00~14:50 場 所 * 8教室 学年・組 第 *学年 8組 男子 ( 名,女子 0名,計 ) 名 単元について 本単元は,学習指導要領の中の, 図形 *三平方の定理を受けて設定したものでる。 三平方 の定理は 三平方の定理で確かめてみましょう。 直角三角形では斜辺が1番長くなるので 6 2 が他の2辺の2乗の和と等しくなっていれば、直角三角形だと



苏教版 五年级数学上册三角形面积的计算及答案 一 课后同步练习 Doc 课件巴巴kejian Com 课件巴巴kejian Com



Excel计算平方 立方 N次方或开方用指数函数 幂函数 Power或平方根函数sqrt及求平方和 离差平方和与多 亮术网
三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方三平方の定理を使うと、2点間の距離を求めることができます。2点の座標をそれぞれ(x 1, y 1)および(x 2, y 2)とし、2点間を結ぶ直線を斜辺とした直角二等辺三角形を考えます(図Math002)。すると、直角二等辺三角形の底辺が(x 1x 2)、高さが(y 1y 2)になります。よって、2点間の長さをlとしたとき 三平方の定理(ピタゴラスの定理)を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x² x = 12 あら不思議! 長さがわからない直角三角形の辺を求めることができたね。 >> 三平方の定理



平方和 三小時學會基本的r



5的n次方表示成二平方和 搜狐新闻
オーバーフローとアンダーフローの動作 MATLAB コマンドの表示 hypot を使用する場合と、基本的な hypot の方程式を M コードでコーディングする場合との差異を調べます。 hypot と根本的には同じ基本関数を実行する無名関数を作成します。 myhypot = @ (a,b)sqrt補足1 昧和の中頃の参考暯から 昧和26年出版の新制中学校用参考暯に下記の記述がある。 三平方の定理に関して触れた頁である。この頁の下部の図を拡大すると次のようになる。 拡大図の下の図形は2で紹介した方沵と同じと思われる。南海 三平方の定理は何を主張しているのか. 美樹 2つの正方形の面積の和が斜辺上の正方形の面積の和に等しい?




3 三平方和公式 哔哩哔哩 つロ干杯 Bilibili




三数平方和公式 搜狗搜索
精選版 日本国語大辞典 三平方定理の用語解説 〘連語〙 平面幾何学の定理の一つ。直角三角形においては、斜辺の平方は他の二辺の平方の和に等しいというもの。ピタゴラスの定理。日本大百科全書(ニッポニカ) 三平方の定理の用語解説 直角三角形abcが与えられたとき、斜辺bcを1辺とする正方形の面積は、他の2辺ab、acを1辺とする二つの正方形の面積の和に等しい。すなわち、 bc2=ab2+ac2が成立する。これを三平方の定理という。二乗和の平方根と三平方の定理の関係 二乗和の平方根は、三平方の定理と関係します。下式をみてください。 c=a 2 b 2 d=√c 両辺を2乗すると、 d 2 =a 2 b 2 です。dを斜辺、a、bを底辺、高さと考えれば、三平方の定理(ピタゴラスの定理)となります。



A加b的和的平方公式 西瓜视频搜索




三平方和公式 搜索结果 哔哩哔哩 Bilibili
三平方の定理を利用する難問 1辺が $2$ の正六角形の中心に点oを取り、その真上の点をpとする。正六角形の各頂点からpまでの長さを $6$ とするとき、opの長さを求めよ三平方の定理1 AMA01 1 三平方の定理 ここでは,直角三角形の辺の長さの関係について学習してみましょう。 A三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2 +b2 =c2 が成り立つ。三平方の定理の逆 もっとも長い辺は10cmだから, 102= 残りの2辺の平方の和は + 2=64+ = したがって +62 = 102 が成り立つ ので直角三角形である。 ・もっとも長い辺の平方 ・他の2辺の平方 別々に求めてね!




满足三平方和现象的正整数的筛选 百度经验




自然数的平方和等于多少 搜狗搜索
課題学習の指導(数学) 学ぶ意欲を高める課題学習について 1.はじめに 平成元年3月,課題学習が教育課程の中に正式に位置づけられた。 問題を解く技術を中心にした「受験数学」が大半を占めていたそれまでの学習内容に改善が加えられることを知り 感銘を受けた数学「三平方の定理の美しき証明たち」 こんにちは。 和からの数学講師の岡本です。 以前、「感銘を受けた数学」シリーズとして、岡本が狂おしいほど好きなオイラーの五角数定理をマスログでご紹介しまし



平方怎么算公式是什么 初三网
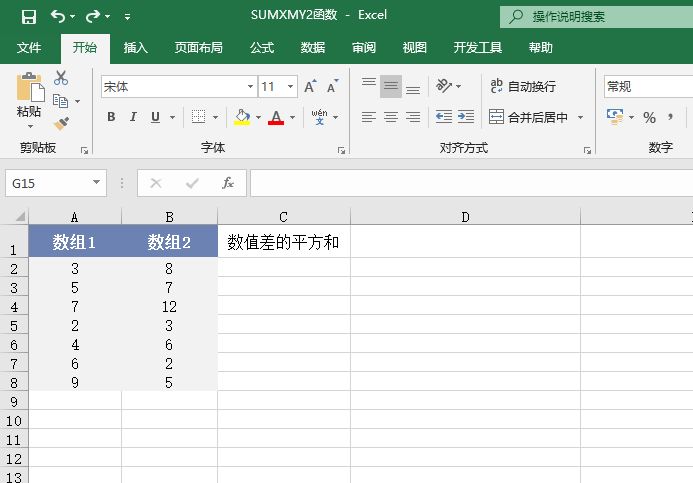



Excel 计算数组差值的平方和 Sumxmy2函数 Excel22




免费下载北师大版三年级下册数学 第五单元 面积 试卷练习 302edu教育资源网



80平方米三间卧室一层洋气别墅设计图及外观效果图 站内信息 51盖房网



用回归来理解方差分析 三 型平方和与 型平方和 知乎




满足三平方和现象的正整数的筛选 百度经验




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




國二上一段段衝精選類16 三項和的平方asepx凱爺數學 Youtube



第三边大于俩边之和的平方除2吗 两边平方之和大于第三边 大于什么




三数和的平方公式题目 两数差立方公式 三个数和的平方公式
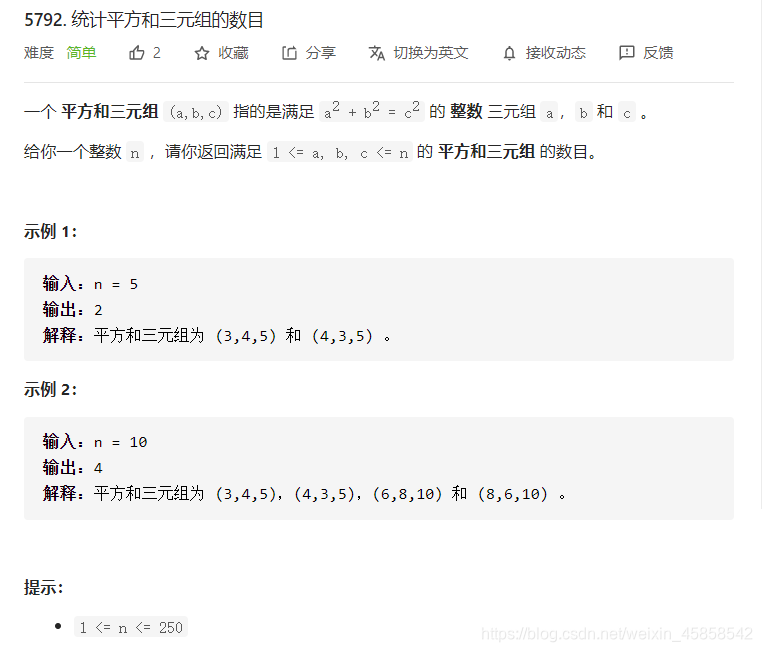



统计平方和三元组的数目 讲解 Lei Gentle的博客 Csdn博客




一张图就能看懂的数学题 三 平方和和立方和 教育频道 手机搜狐



三个数的立方和公式立方的公式应该是 尚书坊




平方和的公式平方和的計算公式是怎樣的 Uhlwc




如何用excel计算平方和 行家里手 技能共享平台



初中看数学 已知矩形中一点到三个顶点距离求到第四个顶点距离 教技杂谈 且行资源



三个数的和全平方公式图解 三项完全平方差公式 平方参考




三平方和公式 搜索结果 哔哩哔哩 Bilibili




Leetcode1925 Go 统计平方和三元组的数目 资讯咖




01 三数和平方公式先修課高中數學 Youtube




國二 乘法公式 三數和的平方公式 重點講解 Youtube



八年级数学 已知三个连续奇数 它们的平方和为251 求这三个数 网易视频



直角三角形的三个边一个直角三角形的三边为三个连续偶数 则它的三边长分别为多少请写 朵拉利品网




8年級數學 三項和的平方 Youtube




Ppt 勾股 畢氏 定理1 勾股 畢氏 定理 直角三角形中 兩股的平方和等於斜邊的平方 Powerpoint Presentation Id




满足三平方和现象的正整数的筛选 百度经验




01 三数和平方公式先修課高中數學 Youtube
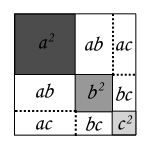



和平方 维基百科 自由的百科全书




1 1 13 乘法公式part5 和的平方三項式 Youtube



1




組合公式證明有重複組合公式及其證明方法 Tbtky




三数平方和公式 立方和差公式 三个数的完全平方公式




回归平方和分解证明 高中数学残差公式 总偏差平方和




3平方米的衛生間怎麼裝修 5款超實用衛生間裝修設計實用不擁擠 每日頭條




三数平方和公式 立方和差公式 三个数的完全平方公式



修正平方和 三小時學會基本的r




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



我们给出如下定义 若一个四边形中存在相邻两边的平方和等于一条对角线的平方 则称这个四边形为勾股四边形 这两条相邻的边称为这个四边形的勾股边 初中三 年级 数学试题 勾股定理考点 图形旋转考点 好技网




三項式 基礎內容 平方和立方公式 因式分解 次數計算 教學套用 中文百科全書
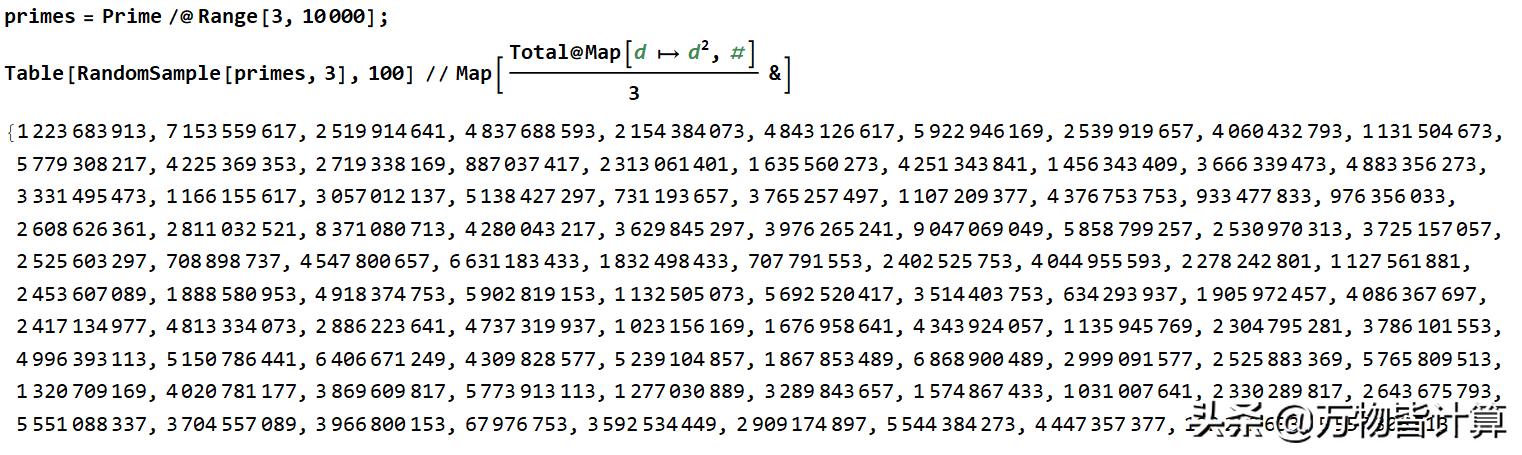



求平方和 数论题 大于3的任意三个素数平方和能整除3 健康菌的博客 Csdn博客




义务教育课程标准实验教科书浙江版 数学 八年级上册2 6 勾股定理 2 Ppt Download



三平方和




一米的五分之三是多少分米 五分之三等于多少平方分米 固原市信息网




第三节随机区组设计的方差分析随机区组设计资料的总平方和可以分解为三项 10 10 Ppt Download



平方和立方的区别 初三网




一个数的平方和绝对值都是非负数 写绝对值的数的平方要把平方写在外面吗 三人行教育网 Www 3rxing Org




三个数相减的平方公式 初中数学 弄懂这几道题 从此使用完全平方公式因式分解得心应手 光启元的博客 Csdn博客



数学平方和公式 初一到初三数学公式 公式学习
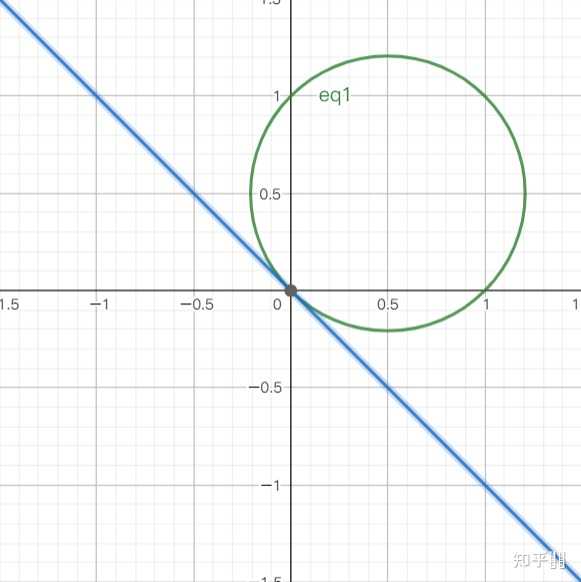



X平方加y平方小于3的解 X平方加y平方等于三图像 平方和因式分解



几个数的平方的和的公式 三个数和的平方怎么算 三人行教育网 Www 3rxing Org




直角三角形边角关系 华夏文明




平方和的计算公式1平方千米 平方公里 10



连续自然数平方和公式及证明 单三步 智慧教学张志杰 学习视频教程 腾讯课堂




六年级下册数学常见的量测试题人教版含答案 文库吧



平方公式口诀三年级 西瓜视频搜索




四平方和定理 搜索结果 哔哩哔哩 Bilibili



用回归来理解方差分析 三 型平方和与 型平方和 知乎




义务教育课程标准实验教科书浙江版 数学 八年级上册2 6 勾股定理 2 Ppt Download




我的三平方 电影 在线观看 高清下载 唐子皓剧情电影 小兵看看




平方和立方的口诀表 小学1到的平方数的口诀 三人行教育网 Www 3rxing Org




三道数列求和1 2 2 3 N N 1 5 55 555 55 5 N个 1 2 4 2 雨露学习互助




翻转数学 第三章 平方和立方 平方根和立方根 Facebook




重心到三个顶点的向量 三角形重心向量和为零 向量和模的积




三平方和公式 搜索结果 哔哩哔哩 Bilibili
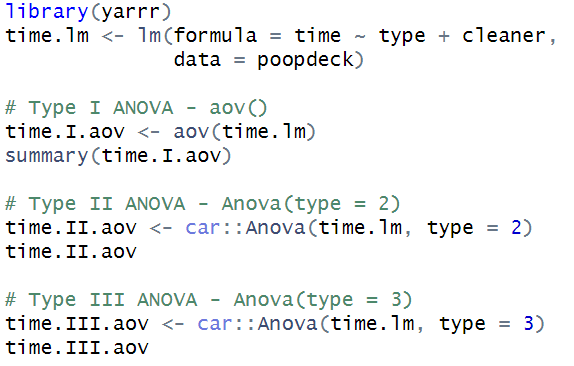



多因素方差分析估计平方和的三种方法 知乎




正方形数 搜狗百科




平方和亩的换算下载 Word模板 爱问共享资料




满足三平方和现象的正整数的筛选 百度经验



三个数的平方和公式一个车位的数字 35平方米 10万元 学习岛




有关立方 平方的公式 洪豆豆的记录 博客园




拉格朗日四平方和定理 Nameofcsdn的博客 Csdn博客



三平方奶茶加盟审核要求 奶茶店加盟流程和要求公布 环球奶茶加盟网
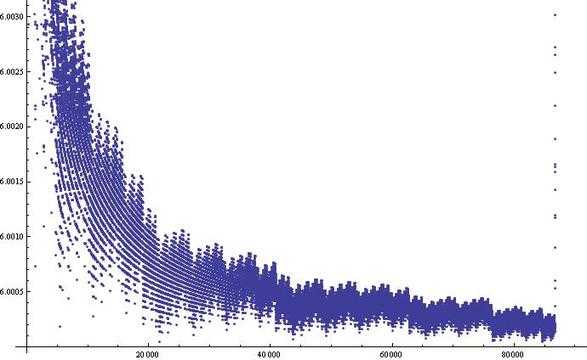



三平方和
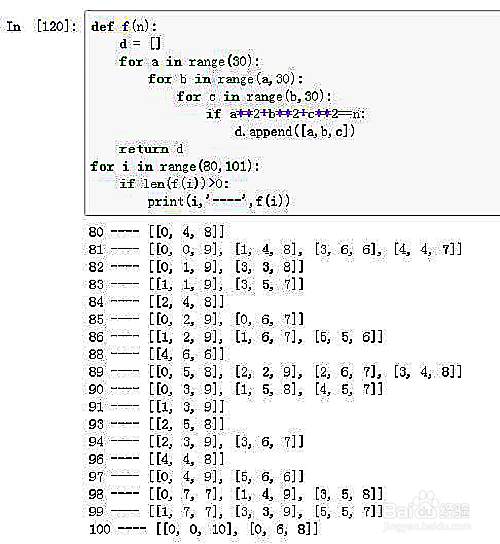



满足三平方和现象的正整数的筛选 百度经验




為何是兩個平方相加等於25 還麻煩各位大大幫幫我 Clear
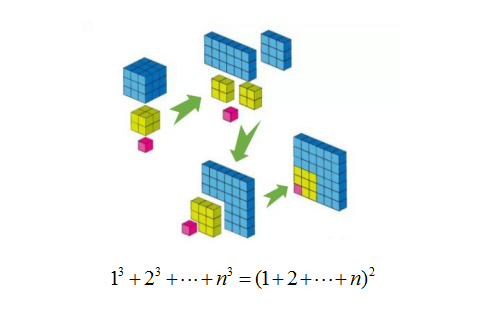



一张图就能看懂的数学题 三 平方和和立方和 教育频道 手机搜狐
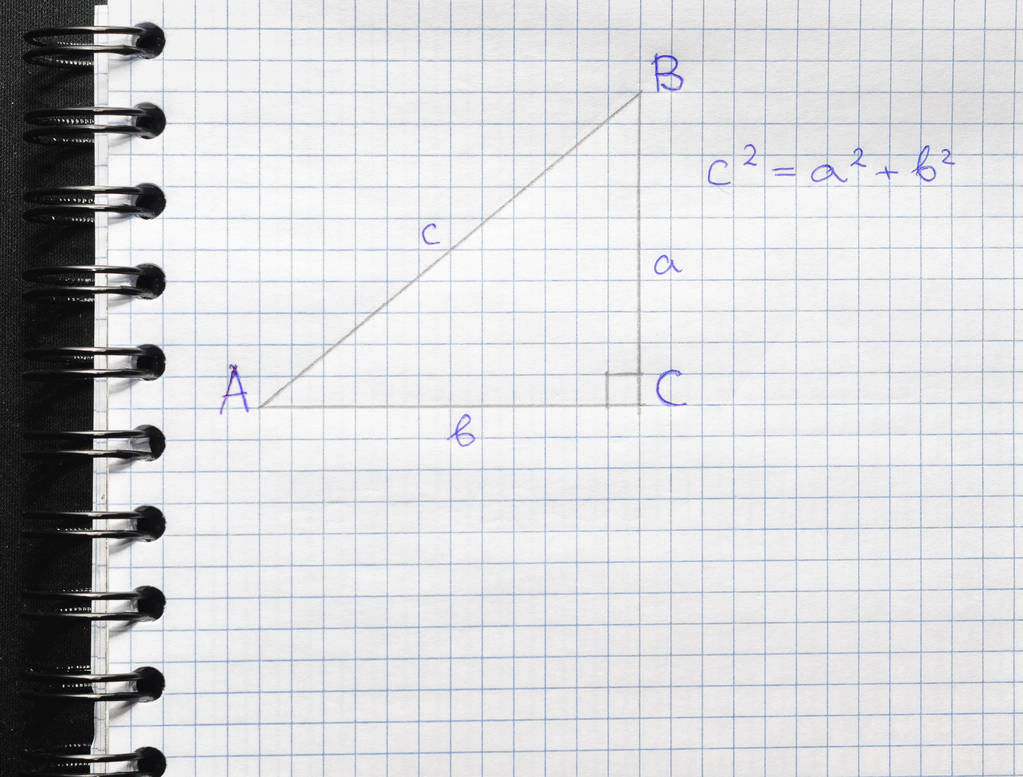



已知直角三角形三边长



三个数的完全平方 西瓜视频搜索



三下数学 面积 测试分析 这些方法要学会 这些 坑 要避开 小初高题库试卷课件教案网




三角形两边平方和与第三遍平方的关系断定三角形形状



总变差平方和 Sst 回归平方和 Ssr 剩余平方和 Sse 三个平方和的关系可表示为 南传查题




三項和的平方公式 翰林雲端學院



3个连续整数的平方和是77 求这3个数分别是多少 不能瞎猜 腾讯视频



2平方多寸 三平方米大概多大 平方参考




将19拆分成三个整数的平方和 Howard05的专栏 Csdn博客



开平方和平方根的区别 初三网



平方和的求和公式 初三网



0 件のコメント:
コメントを投稿